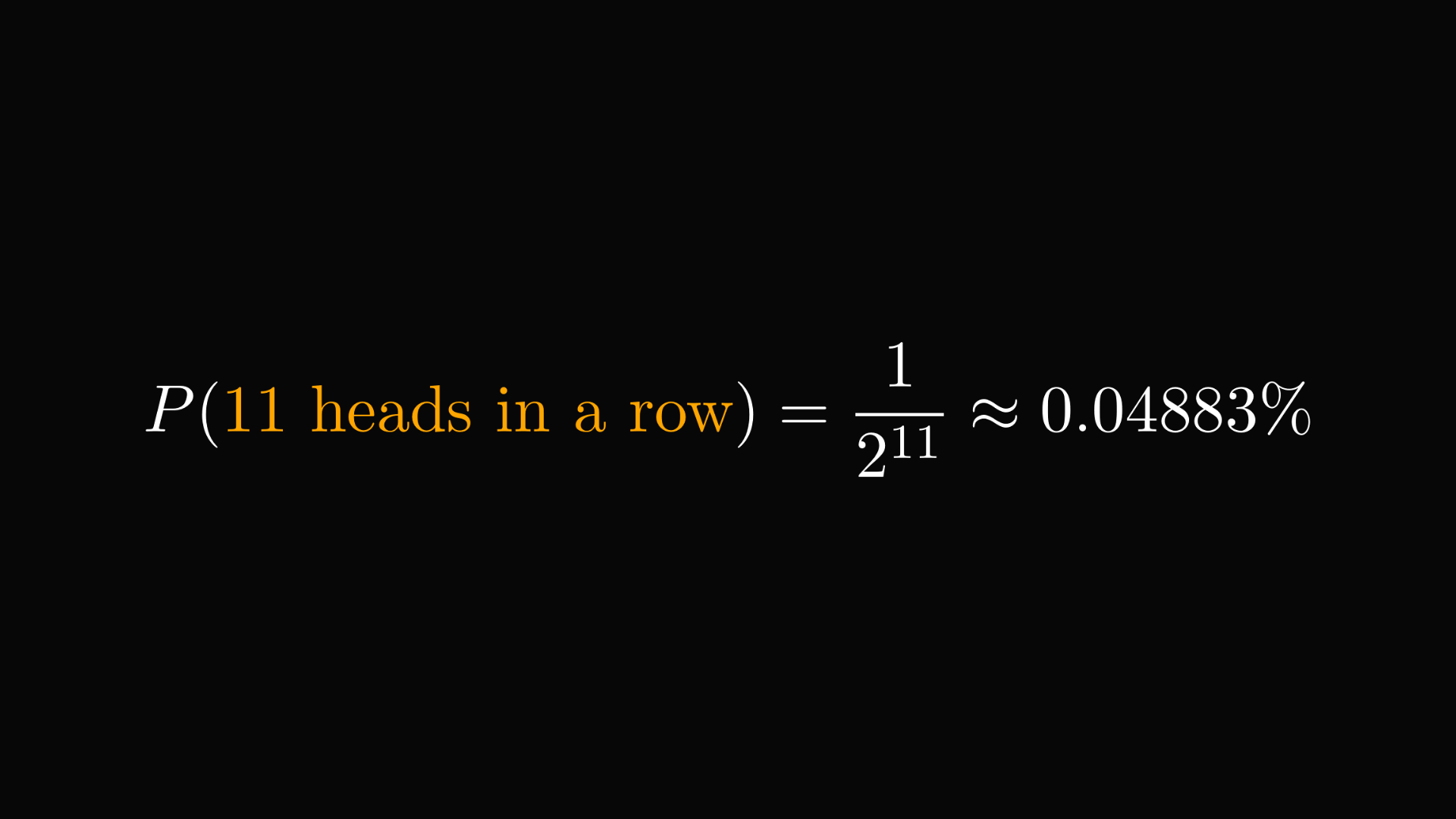Our intuition about probability is horrible, and it can easily lead us to financial ruin.
Gamblers on a losing streak tend to keep on playing, as they perceive that their bad luck should increase the chance of winning.
Here is why this is wrong.
Let's play a simple game!
The dealer tosses a fair coin. If it comes up tails, you win . Heads, you lose .
Suppose that you lost ten times in a row. Does it make winning the next round more likely?
Without any extra information, the probability of eleven heads in a row is tiny.
However, this was not our case. The original question was to find the probability of the eleventh toss, given the result of the previous ten.
In statistics, we study events in the context of other events. This is captured by conditional probabilities, answering a simple question: "what is the probability of if we know that has occurred?". (If you are not familiar with conditional probabilities, check out my recent post explaining it in detail!)
In fact, none of the previous results influence the current toss. I could have tossed the coin thousands of times and it all could have come up heads. None of that matters.
Coin tosses don't remember each other. So, we still have that the -th toss comes up heads.
The notion of independence formalizes this concept. By definition, and are independent if observing doesn't change the probability of .
Despite this, people often perceive that certain past events influence the future. This is not the case in gambling.
If I lose hands of Blackjack in a row, it doesn't mean that I ought to be lucky soon. Hence, this phenomenon is called the gambler's fallacy.
You can test this for yourself with Python. I simulated a thousand independent coin tosses and highlighted where I got ten heads in a row.
In practice, we use runs of matching outcomes to determine if a sequence is truly random. The lack of "streaks" indicates a lack of randomness. This is the so-called Wald–Wolfowitz runs test.
 Tivadar Danka
Tivadar Danka