Why is linear algebra essential in machine learning?

For every topic in computer science, there is an XKCD comic that summarizes it perfectly. My all-time favorite one is the following.

All jokes aside, linear algebra plays a crucial part in machine learning. From classical algorithms to state-of-the-art, it is everywhere. This post is about why.

Data = vectors

As you probably know, data is represented by vectors.

Data points are just tuples of measurements. In their raw form, they are hardly useful for us. They are just blips in space.

Without operations and transformations, it is difficult to predict class labels or do anything else.

Vector spaces provide a mathematical structure where operations naturally arise. Instead of a blip, just imagine an arrow pointing to the data point from a fixed origin.

On vectors, we can easily define operations using our geometric intuition. Addition is translation, while scalar multiplication is scaling.

Why do we even need to add data points together?

To transform raw data into a form that can be used for predictive purposes. Raw data can have a really complicated structure, and we aim to simplify it as much as possible. For instance, raw data is often standardized by subtracting the mean of features and scaling with their variance. This way, each feature is of the same magnitude, making sure that none of them are dominated by the ones on the largest scale.

Aside from the operations, vector spaces give rise to linear transformations. They are essentially distortions of the vectors space, yielding a new set of features for our dataset. We are going to take a detailed look at them below.

Machine learning algorithms are functions

In essence, a machine learning model works by doing the following two things.

1. Find an alternative representation of the data.
2. Make decisions based on this representation.

Linear algebra plays a role in describing and manipulating those representations, may it be the raw data or a high-level feature set.

Regardless of the features, data points are given by vectors. Finding more descriptive representations is the same as finding functions mapping between vector spaces. The simplest ones are the linear transformations given by matrices.

$$f(x) = Ax, \quad x \in \mathbb{R}^n, \quad A \in \mathbb{R}^n.$$

Why do we love linear transformations? First, they are easy to work with and fast to compute. Moreover, combined with simple nonlinear functions, they can create expressive models.

Linear transformations = transformations of data

How does a linear transformation transform the data? To see this, the only thing we need to notice is that the images of the basis vectors completely determine a given linear transformation.

Linearity means that the order of addition, scalar multiplication, and function application can be changed. So, the image of every vector is a linear combination of the images of the basis vectors.

To be mathematically precise, this is what happens:

$$\begin{align*} f(x) &= f\bigg( \sum_{i=1}^{n} x_i e_i \bigg) \\ &= \sum_{i=1}^{n} x_i f(e_i). \end{align*}$$

We can visualize this for linear transformations on the two-dimensional plane.

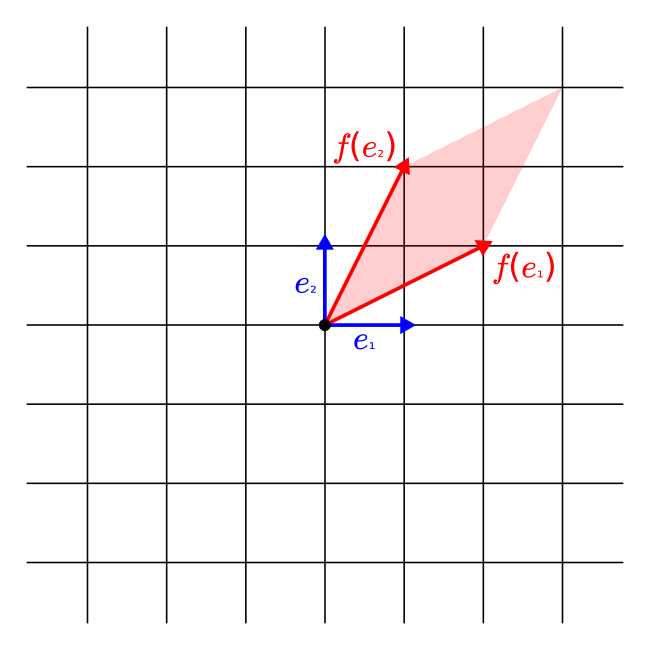
As you can see, the images of the basis vectors form a parallelogram. (Whose sides can fall onto a single line.) From yet another perspective, this is the same as distorting the grid determined by the basis vectors.

Finding more descriptive representations

How can a linear transformation help to find better representations of the data?

Think about PCA, which finds features with no redundancy. This is done by a simple linear transformation. (If you are not familiar with how PCA works, check out my recent article about it!)

So, linear transformations give rise to new features. How descriptive can these be?

For instance, in classification tasks, we want each high-level feature to represent the probability of belonging to a given class. Are linear transformations enough to express this?

Almost.

Any true underlying relationship between data and class label can be approximated by composing linear transformations with certain nonlinear functions (such as the Sigmoid or ReLU).

This is formally expressed by the Universal Approximation Theorem.

This is why machine learning is just a pile of linear algebra, stirred until it looks right. (Not just accordingly to XKCD.) In summary, linear transformations are

• simple to work with,
• fast to compute,
• and can be used to build powerful models.